贝塞尔曲线(植物大战僵尸的补充)

局部路径规划算法

贝塞尔算法思想

贝塞尔曲线是应用于二维图形应用程序的数学曲线，由一组称为控制点的向量来确定，给定的控制点按顺序连接构成控制多边形，
贝塞尔曲线逼近这个多边形，进而通过调整控制点坐标改变曲线的形状。
对于车辆系统,规划的轨迹应该满足以下准则:轨迹连续,轨迹曲率连续,轨迹容易被车辆跟踪,而且容易生成;
给定n+1个数据点,p0-pn,生成一条曲线,使该曲线与这些点描述的形状相符;

推导

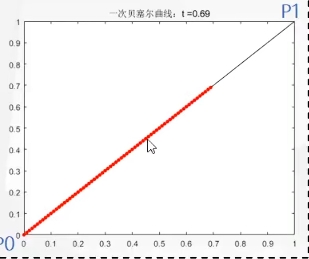
一次贝塞尔曲线

设\(P_0\)，\(P_1\)两个控制点，t取值范围为\([0,1]\)。
直线
则贝塞尔曲线生成点可以表达为：\(p_1(t) = (1 - t)P_0 + tP_1\)
t可以为时间
1

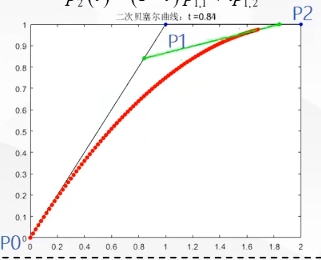
二阶

设P0，P1，P2三个控制点，t取值范围为\([0,1]\)。\(P_0\)和\(P_1\)构成一阶，
\(P_1\)和\(P_2\)也构成一阶，即：\(\begin{cases}
$p_{1,1}(t) = (1 - t)P_0 + tP_1 \\ p_{1,2}(t) = (1 - t)P_1 + tP_2 \end{cases})在生成的两个一阶点基础上，可以生成二阶贝塞尔点：在生成的两个一阶点基础上，可以生成二阶贝塞尔点：(p_2(t) = (1 - t)p_{1,1} + tp_{1,2})$
1

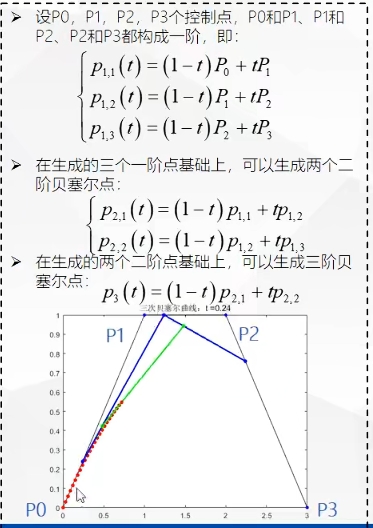
三阶

1